다익스트라 알고리즘은 음의 가중치가 없는 그래프의 한 노드에서 각 모든 노드까지의 최단거리를 구하는 알고리즘이며 도로 교통망 같은 곳에서 나타날 수 있는 그래프에서 두 노드 간의 최단경로를 찾는 알고리즘이기도 하다.
(무방향/ 방향그래프 둘다 상관없이 사용가능하다)
해당 알고리즘은 DP(다이나믹 프로그래밍)와 Greedy Algorithm(탐욕 알고리즘)을 복합적으로 사용하는 알고리즘이다.
최단거리는 여러개의 최단거리로 나눠져있고 이전까지 구한 최단 거리는 그대로 사용한다 → DP
눈앞에 보이는 최적의 선택을 한다 → Greedy
예시를 들면서 한번 다익스트라로 어떻게 풀어나가는지 확인해보고 마무리 지어보겠습니다.
예시 네비게이션
1번에서 6번을 최단 경로로 찾아가야하는 상황에서 모든 노드까지의 최단거리를 구하는 알고리즘을 설계해보겠습니다.

1) 1번노드에서 연결된 간선기준으로 최단 거리(빨간색)를 측정을 합니다. 모르는 지역은 무한으로 설정합니다.
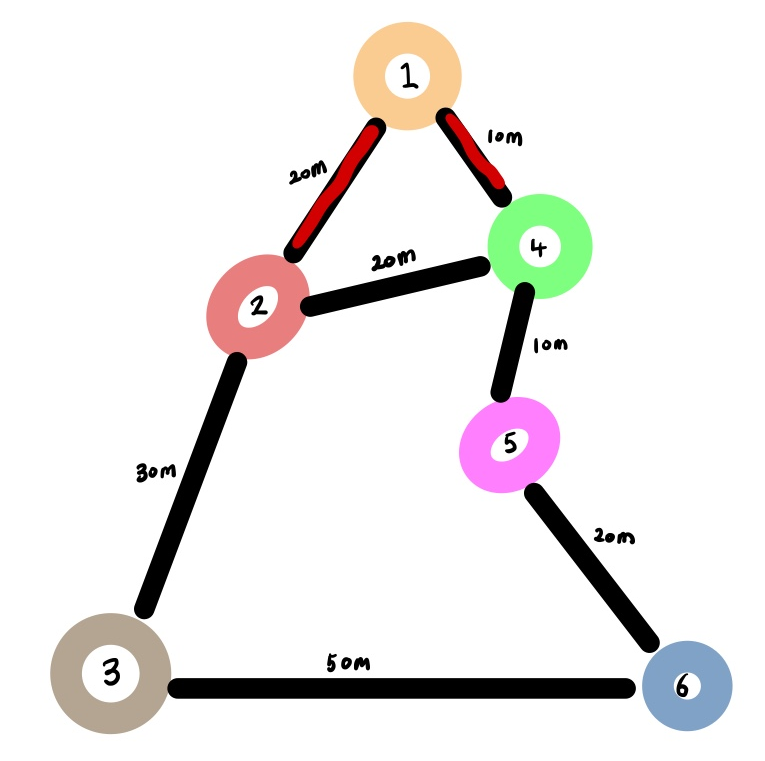
| 정점 | 1(고정) | 2 | 3 | 4 | 5 | 6 |
| 거리 | 0 | 20 | 무한 | 10 | 무한 | 무한 |
2) 그후 제일 거리가 낮은 4번노드로 이동하고 값을 고정합니다.
새로 연결된 간선기준으로 최단 거리(빨간색)를 측정을 하고 새로운 경로에 대해서 최단거리인지 확인후 아니므로 갱신을 하지 않습니다.(1->2 파란색 : 10 + 20 m < 빨간색: 20m)
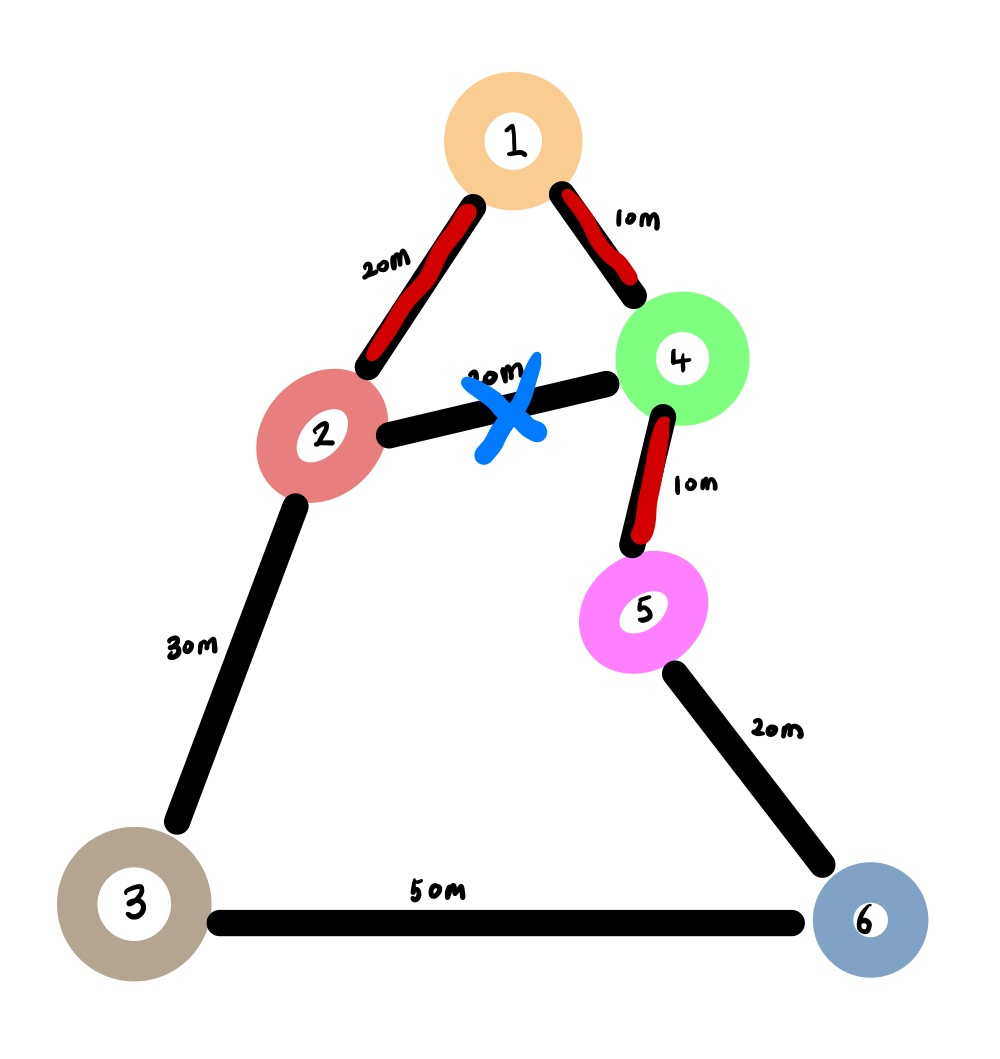
| 정점 | 1(고정) | 2 | 3 | 4(고정) | 5 | 6 |
| 거리 | 0 | 20 | 무한 | 10 | 20(10+10) | 무한 |
3) 이어서 제일 거리가 낮은 2번노드로 이동하고 값을 고정합니다.
새로 연결된 간선기준으로 최단 거리(빨간색)를 측정을 합니다
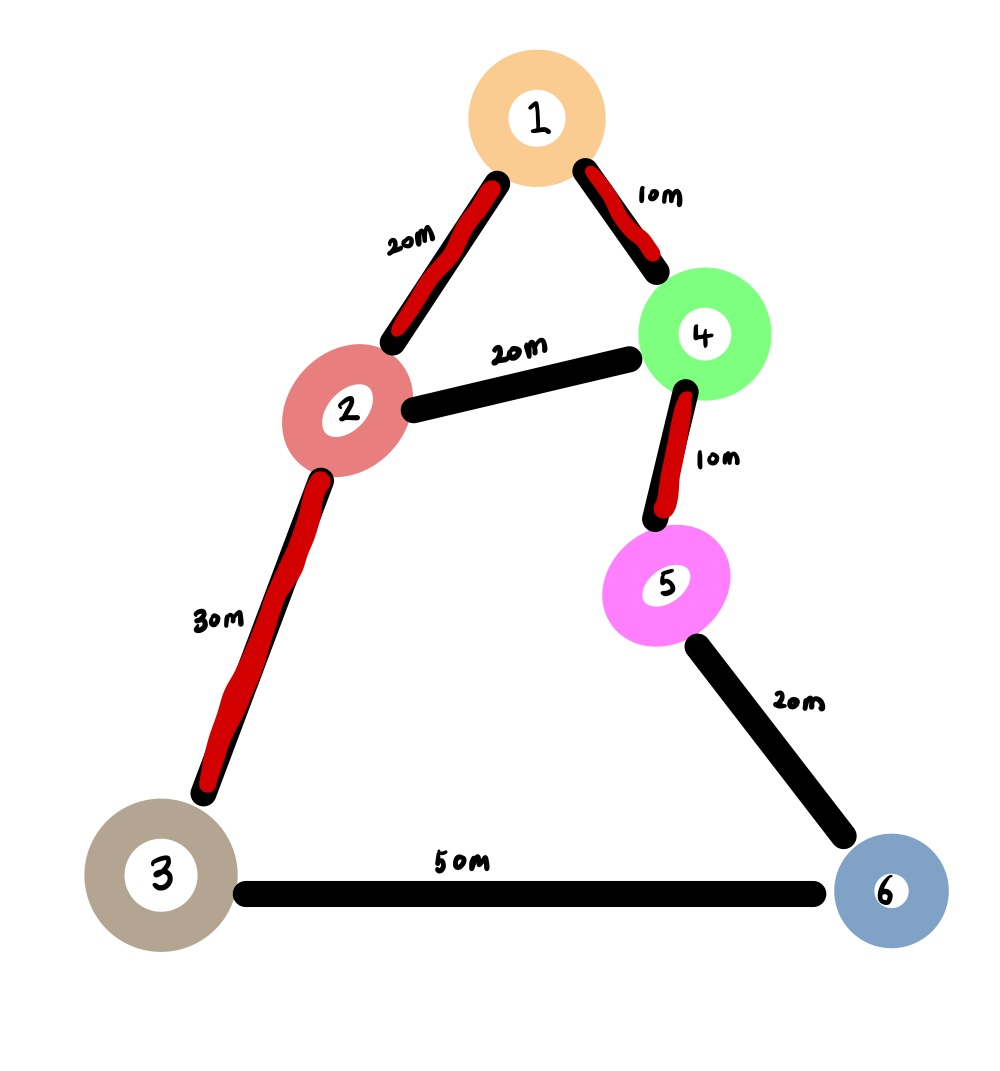
| 정점 | 1(고정) | 2(고정) | 3 | 4(고정) | 5 | 6 |
| 거리 | 0 | 20 | 50(20+30) | 10 | 20(10+10) | 무한 |
4) 그다음 제일 거리가 낮은 5번노드로 이동하고 값을 고정합니다.
새로 연결된 간선기준으로 최단 거리(빨간색)를 측정을 합니다.

| 정점 | 1(고정) | 2(고정) | 3 | 4(고정) | 5(고정) | 6 |
| 거리 | 0 | 20 | 50(20+30) | 10 | 20(10+10) | 40(10+10+20) |
5) 또 제일 거리가 낮은 6번노드로 이동하고 값을 고정합니다.
새로 연결된 간선기준으로 최단 거리(빨간색)를 측정을 하고 새로운 경로(파란색)에 대해서 최단거리인지 확인후 아니므로 갱신을 하지 않습니다
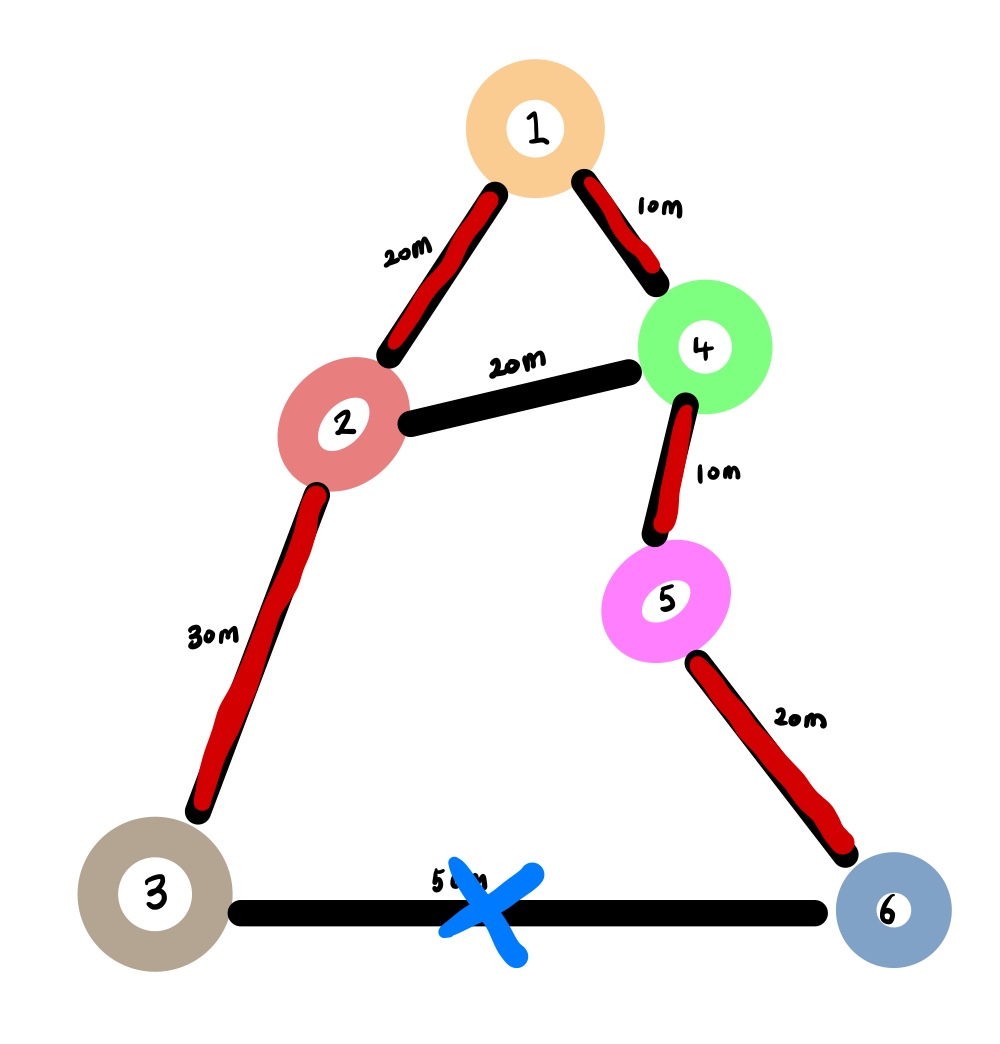
| 정점 | 1(고정) | 2(고정) | 3 | 4(고정) | 5(고정) | 6(고정) |
| 거리 | 0 | 20 | 50(20+30) | 10 | 20(10+10) | 40(10+10+20) |
6) 그후 마지막 3번으로 이동하고 고정하면 최단거리가 확인이 된다.
| 정점 | 1(고정) | 2(고정) | 3(고정) | 4(고정) | 5(고정) | 6(고정) |
| 거리 | 0 | 20 | 50(20+30) | 10 | 20(10+10) | 40(10+10+20) |
동작 과정을 간단하게 풀면 아래와 같다
1. 특정 노드를 선택
2. 선택하지 않은 노드들 중 최단 거리의 노드 선택
3. 모든 노드들이 선택될 때까지 2번 과정을 반복
여기서 알 수 있는 점은 한번 방문한 노드는 재방문을 하지 않는다는 점이고 프림알고리즘과 비슷하다는 점을 알 수있다.
시간복잡도
최소 비용 노드을 선택하는 과정은 선형탐색을 이용하면 최악의 경우
모든 노드을 확인해야 하므로 O(V²)의 시간복잡도를 가지게 된다.
힙으로 구현하게 되면 O(ElogV)이며
피보나치 힙 우선순위 큐를 이용하게 될경우 O(E+VlogV)를 가지게된다
응용 코드
다익스트라를 2가지로 이용할 수있는데
시작점에서 모든 최적거리 를 확인하는 방법과
시작점에서 종점까지 최적루트를 확인하는 코드를 만들 수 있다.
1. 시작점에서 모든 최적거리 링크
import heapq
def dijkstra(graph, start):
# 시작 정점으로부터의 최단 거리를 저장할 딕셔너리
distances = {vertex: float('infinity') for vertex in graph}
distances[start] = 0
# 최단 거리가 확정된 정점들의 집합
visited = set()
# 최단 거리를 갱신할 수 있는 간선들을 저장할 우선순위 큐
queue = [(0, start)]
while queue:
# 현재 정점까지의 최단 거리와 정점을 가져옴
current_distance, current_vertex = heapq.heappop(queue)
# 이미 방문한 정점이면 스킵
if current_vertex in visited:
continue
# 현재 정점을 방문한 것으로 표시
visited.add(current_vertex)
# 현재 정점과 연결된 정점들을 순회하며 최단 거리를 업데이트
for neighbor, weight in graph[current_vertex]:
distance = current_distance + weight
# 현재 정점을 통해 다른 정점으로 가는 거리가 더 짧으면 업데이트
if distance < distances[neighbor]:
distances[neighbor] = distance
heapq.heappush(queue, (distance, neighbor))
return distances
# 예제 그래프
graph = {
'1': [('2',20), ('4', 10)],
'2': [('1', 20), ('3', 30), ('4', 20)],
'3': [('2', 30), ('6', 50)],
'4': [('1', 10), ('2', 20), ('5', 10)],
'5': [('4', 10), ('6', 20)],
'6': [('3', 50), ('5', 20)],
}
# 시작 정점
start_vertex = '1'
# 다익스트라 알고리즘 수행
shorts = dijkstra(graph, start_vertex)
# 결과 출력
print("시작 정점으로부터의 최단 거리:")
for vertex, distance in shorts.items():
print(f"정점 {vertex}: {distance}")
2. 시작점에서 종점까지 최적루트 링크
import heapq
def dijkstra(graph, start):
# 시작 정점으로부터의 최단 거리를 저장할 딕셔너리
distances = {vertex: float('infinity') for vertex in graph}
distances[start] = 0
# 최단 거리가 확정된 정점들의 집합
visited = set()
# 최단 거리를 갱신할 수 있는 간선들을 저장할 우선순위 큐
queue = [(0, start)]
while queue:
# 현재 정점까지의 최단 거리와 정점을 가져옴
current_distance, current_vertex = heapq.heappop(queue)
# 이미 방문한 정점이면 스킵
if current_vertex in visited:
continue
# 현재 정점을 방문한 것으로 표시
visited.add(current_vertex)
# 현재 정점과 연결된 정점들을 순회하며 최단 거리를 업데이트
for neighbor, weight in graph[current_vertex]:
distance = current_distance + weight
# 현재 정점을 통해 다른 정점으로 가는 거리가 더 짧으면 업데이트
if distance < distances[neighbor]:
distances[neighbor] = distance
heapq.heappush(queue, (distance, neighbor))
return distances
# 예제 그래프
graph = {
'1': [('2',20), ('4', 10)],
'2': [('1', 20), ('3', 30), ('4', 20)],
'3': [('2', 30), ('6', 50)],
'4': [('1', 10), ('2', 20), ('5', 10)],
'5': [('4', 10), ('6', 20)],
'6': [('3', 50), ('5', 20)],
}
# 시작 정점
start_vertex = '1'
# 도착 정점
end_vertex = '6'
shorts = dijkstra(graph, start_vertex)# 다익스트라 알고리즘 수행
short= shorts[end_vertex] # 도착 정점까지의 최단 거리와 경로
# 결과 출력
print(f"{start_vertex}에서 {end_vertex}까지의 최단 거리: {short}")
# 경로 출력
current_vertex = end_vertex
path = [current_vertex]
while current_vertex != start_vertex:
for neighbor, weight in graph[current_vertex]:
if shorts[current_vertex] == shorts[neighbor] + weight:
path.append(neighbor)
current_vertex = neighbor
break
path.reverse()
print(f"{start_vertex}에서 {end_vertex}까지의 최단 경로: {' -> '.join(path)}")
관련된 포스팅
'3.4. 프로그래밍 개념 및 도구 > 알고리즘 이론' 카테고리의 다른 글
| [Algorithm] 허프만 코드 (0) | 2024.04.08 |
|---|---|
| [Algorithm] Scheduling (0) | 2024.04.08 |
| [Algorithm] 최소 신장 트리(MST), Kruskal & Prim algorithm (0) | 2024.04.07 |
| [Algorithm] Greedy Algorithm (0) | 2024.04.07 |
| 3 다이나믹 프로그래밍(Dynamic Programming : DP/동적계획) (0) | 2024.04.07 |



댓글