목차
1. Greedy Algorithm?
2. 대표적인 Greedy
3. 코드모음 _링크_
Greedy Algorithm이란?
Greedy Algorithm(이하 Greedy) 말 그대로 탐욕스럽게 현재 '가장 좋아 보이는' 답(최선의 선택)을 선택하는 알고리즘
Greedy는 DP(동적프로그래밍)을 간단한 문제 해결에도 지나치게 많은 일을 하는 문제점을 해결하고자 고안되었다.
최선의 선택은
선택할 당시에 가장 좋은 것을 선택하는 것을 의미합니다
간단하게 예시를 들면 눈앞에 12만원과 18만원이 있다면 18만원을 선택하는 것과 동일합니다.
뒤에 뭐가 있든 최선을 선택하는 것은 좋은 결과물을 보장해줄까요?
한번 예시를 들어보죠 거스름돈 예시입니다.
기존 화폐단위에서 10만원을 큰 화폐부터 거슬러 줘서 적은 장수를 거슬러 주는 알고리즘을 설계하고 돌려보겠습니다.
change = 100000
bills = [50000, 10000, 5000, 1000]
counts = []
for bill in bills:
count = change // bill
counts.append(count)
change -= bill * count
total_bills = sum(counts)
print("각 지폐 사용 개수 :", str(counts))
print("총 지폐 사용 개수 :", str(total_bills))
결과적으로 5만원 2장이 나오고 여러분이 생각하기에도 제일 적은 2장으로 바꿔줬습니다.
만약에 7만원짜리의 화폐가 나와도 최적의 해를 보장해 줄 가요?
change = 100000
bills = [70000, 50000, 10000, 5000, 1000]
counts = []
for bill in bills:
count = change // bill
counts.append(count)
change -= bill * count
total_bills = sum(counts)
print("각 지폐 사용 개수 :", str(counts))
print("총 지폐 사용 개수 :", str(total_bills))7만원 1장 1만원 3장으로 4장의 화폐로 거슬러 줍니다.
동일한 알고리즘을 사용했음에도 Greedy는 이처럼 현재 상황에서 가장 좋은 결과를 선택하는 방식이기 때문에
7만원이 1장을 선택할 당시에는 최적의 상황이었지만 최종적인 결과 도출에서는 최적의 해를 보장해주지 않습니다.
(7만원 1장 1만원 3장 = 총 4장 << 5만원 2장 )
Greedy는 최적의 해를 보장해주지 않았습니다.
그럼에도 쓰는이유는 간단한 문제를 복잡하게 해결하지 않기 위해서 사용되며 사용하기에는 조건이 따릅니다
Greedy Algorithm 조건
1. 현재의 가장 좋은 선택이 전체 문제해결에 최적의 해를 반드시 도출해야 한다.
2. 문제 해결도중에서도 여러 단계가 존재하는데, 이 단계 도중에서도 항상 최적의 해를 도출해야 한다.
Greedy는 즉 눈앞에 보이는 탐욕적인 선택을 하는 과정 속에서도 최적의 해를 도출하면서 최종적으로도 최적의 해를 도출해야 합니다.
Greedy의 조건에 대해 대충 판단하고 사용하면 문제가 생깁니다.
즉, Greedy Algoritm은 따라서 검증이 필요합니다
검증방법은 아래와 같습니다
1. 선택과정 : 현재 과정에서 최선을 선택한다.
2. 적절성 검사 : 최선의 선택이 문제의 조건을 만족하는지 검사한다.
3. 해답 점검 : 최종적으로 문제가 해결되었는지 검사하고 해결되지 않았다면, 1. 선택과정으로 돌아가서 과정을 반복한다.
해당 과정을 매번 하여 검증을 하고 Greedy가 적합한지 판단합니다.
2. Greedy의 대표적 종류
Greedy를 매번 설계하기 힘드니까 대표적인 종류를 간단하게 알아보고 적용해보겠습니다.
종류는 아래와 같으며 자세한 포스트는 링크에 정리되어 있습니다.
- 최소비용 신장 트리 (Minimum Spanning Tree : MST) 최소신장 트리(MST), Kruskal & Prim algorithm
- 크루스칼 알고리즘(Kruskal Algorithm)
- 프림 알고리즘(Prim Algorithm)
- 다익스트라 알고리즘(Dijkstra Algorithm) 다익스트라 알고리즘(Dijkstra Algorithm)
- 스케줄 짜기(Scheduling) Scheduling
- 허프만 알고리즘 허프만 코드
3. Greedy vs Dp
대표적인 예시는 도둑문제(배낭채우기)입니다.
여러분은 10Kg를 들수 있는 도둑입니다.
앞에 보이는 책상에 다양한 물건들이 있습니다.
| 물건 | 무게 | 가치 |
| 컴퓨터 알고리즘 책 | 1kg | 500 |
| 노트북 | 10kg | 2000 |
| 아이패드 | 5kg | 1500 |
| 아이폰 | 3kg | 1000 |
가치를 제일 좋게 어떻게 훔칠까요?
Greedy로 해결을 해보겠습니다.
1. 가치기준으로 Greedy 링크
가치가 높은 것부터 먼저 훔치게 설계를 해보겠습니다.
# 물건 종류, 무게, 가치
items = [
('컴퓨터 알고리즘 책', 1, 500),
('노트북', 10, 2000),
('아이패드', 5, 1500),
('아이폰', 3, 1000)
]
# 손에 들 수 있는 무게
hand_limit = 10
# 물건중에 가장 비싼 물건을 선택하는 Greedy
items.sort(key=lambda x: x[2], reverse=True) # 물건을 가치순으로 정렬
total_weight = 0
total_value = 0
stolen_items = []
for item in items:
if total_weight + item[1] <= hand_limit: # 아직 손에 들 수 있는 무게가 남아있는 경우
total_weight += item[1]
total_value += item[2]
stolen_items.append(item[0])
print("훔친 물건:", stolen_items)
print("총 훔친 물건의 가치:", total_value)훔친 물건: ['노트북']
총 훔친 물건의 가치: 2000
코드가 실행되는데 걸린 시간: 0:00:00.000028해당 코드로 돌려보니
노트북을 먼저 훔치고 물건을 훔칠 수가 없기 때문에 끝이납니다
가치는 2000으로 끝이납니다 .
2. 무게 기준으로 Greedy 링크
이번엔 많이 넣을 수 있게 무게가 가벼운 순서대로 설계를 해보겠습니다.
# 물건 종류, 무게, 가치
items = [
('컴퓨터 알고리즘 책', 1, 500),
('노트북', 10, 2000),
('아이패드', 5, 1500),
('아이폰', 3, 1000)
]
# 손에 들 수 있는 무게
hand_limit = 10
#가장 가벼운 물건을 선택하는 탐욕 알고리즘
items.sort(key=lambda x: x[1]) # 물건을 무게순으로 정렬
total_weight = 0
total_value = 0
stolen_items = []
for item in items:
if total_weight + item[1] <= hand_limit: # 아직 손에 들 수 있는 무게가 남아있는 경우
total_weight += item[1]
total_value += item[2]
stolen_items.append(item[0])
print("훔친 물건:", stolen_items)
print("총 훔친 물건의 가치:", total_value)훔친 물건: ['컴퓨터 알고리즘 책', '아이폰', '아이패드']
총 훔친 물건의 가치: 3000
코드가 실행되는데 걸린 시간: 0:00:00.000032
해당 코드로 돌려보니
컴퓨터 알고리즘 책을 먼저 훔치고 아이폰, 아이패드 순으로 훔치고 끝이 납니다.
가치는 3000으로 끝이 납니다.
만약 여기에 1.5kg짜리 새로운 물건인 에어팟을 추가해보면 아이폰 이전에 에어팟을 챙기면서
마지막인 아이패드를 못챙기는 상황이 일어나게 됩니다.
["컴퓨터알고리즘 책", "에어팟","아이폰"] 총 무게 5.5kg로써 아이패드(5kg)를 못챙기는 상황 발생
거스름돈 7만원예시와 동일하게 해당 알고리즘은 에어팟이 추가될때 최선의 해가 아니게됩니다
3. DP로 푸는 도둑문제 링크
def knapsack(items, hand_limit):
# 아이템의 개수와 손에 들 수 있는 최대 무게
n = len(items)
dp = [[0] * (hand_limit + 1) for _ in range(n + 1)]
# 다이나믹 프로그래밍을 통해 최적의 가치를 계산
for i in range(1, n + 1):
for w in range(1, hand_limit + 1):
weight, value = items[i - 1][1], items[i - 1][2]
if weight <= w:
dp[i][w] = max(dp[i - 1][w], dp[i - 1][w - weight] + value)
else:
dp[i][w] = dp[i - 1][w]
# 최적의 가치를 찾기 위해 역추적
total_value = dp[n][hand_limit]
total_weight = hand_limit
stolen_items = []
for i in range(n, 0, -1):
if dp[i][total_weight] != dp[i - 1][total_weight]:
item_name = items[i - 1][0]
stolen_items.append(item_name)
total_weight -= items[i - 1][1]
return stolen_items, total_value
start_time = datetime.now()
# 물건 종류, 무게, 가치
items = [
('컴퓨터 알고리즘 책', 1, 500),
('노트북', 10, 2000),
('아이패드', 5, 1500),
('아이폰', 3, 1000)
]
# 손에 들 수 있는 무게
hand_limit = 10
stolen_items, total_value = knapsack(items, hand_limit)
print("훔친 물건:", stolen_items)
print("총 훔친 물건의 가치:", total_value)훔친 물건: ['아이폰', '아이패드', '컴퓨터 알고리즘 책']
총 훔친 물건의 가치: 3000
코드가 실행되는데 걸린 시간: 0:00:00.000055코드를 돌려보니
최적의 가치가 나왔지만
무게를 정렬하고 무게를 기준으로 모든 경우의수를 구하고 총 가치가 가장 높은 경우의 수가 최적의 답을 도출 하는 방식이므로 걸린 시간은 2배가 걸렸습니다.
만약 똑같이 0.5kg짜리 신문이 있었더라도 아이폰 아이패드 컴퓨터 알고리즘책을 챙기게 최적의 가치가 나오게 계산이됩니다
차이를 한눈에 보면
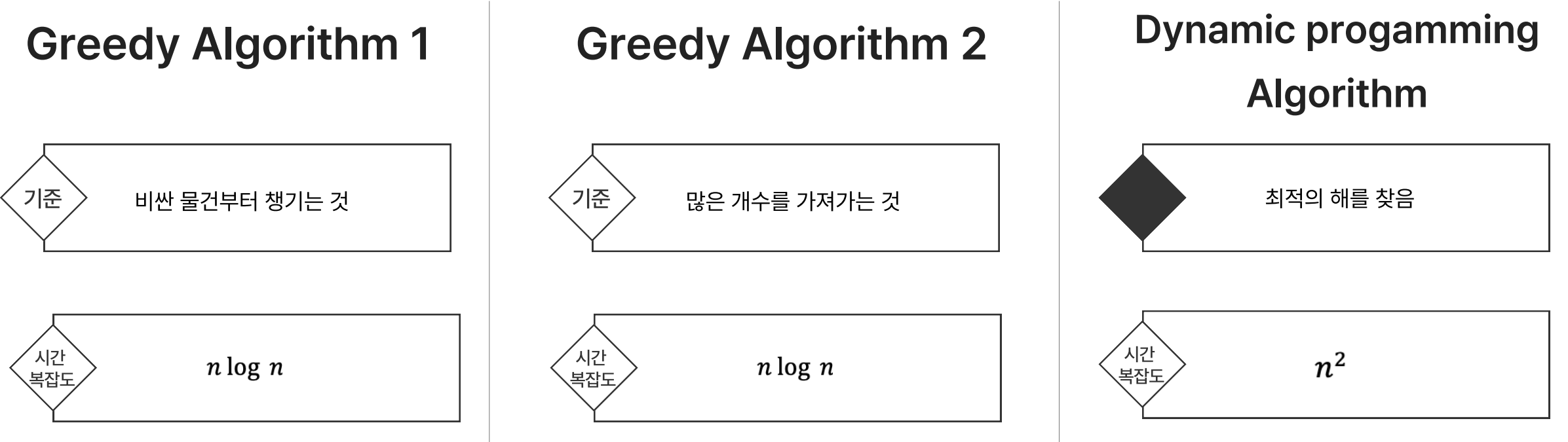
Greedy는 빠르지만 기준을 확실하게 잡고 설계를 해야하므로 특정 문제에 최적화된 문제임을 알수 있습니다.
이러한 점을 알고 개발할 때 다양한 알고리즘을 배워야함을 알 수있고 DP와 Greedy의 차이점을 알 수 있다!
여기서 의문점이 하나 있을 겁니다.
무게당 가치를 기준으로 탐욕을 하면 되는거 아닌가 싶은데
물건항목을 디테일하게 바꾸고 예시를 보면 확실하게 알게됩니다
Greedy (기준: 무게당 가치 탐욕) 링크
from datetime import datetime
def elapsed_time(start_time):
end_time = datetime.now()
elapsed = end_time - start_time
return elapsed
start_time = datetime.now()
# 물건 종류, 무게, 가치
items = [
('아이폰', 2, 1100),
('컴퓨터 알고리즘 책', 1, 400),
('노트북', 10, 2000),
('아이패드프로', 5, 1800),
('아이패드에어', 3, 1500),
('애플워치', 2, 700)
]
# 손에 들 수 있는 무게
hand_limit = 10
# 가방에 넣을 수 있는 가장 비싼 물건을 선택하는 탐욕 알고리즘
items.sort(key=lambda x: x[2]/x[1], reverse=True) # 물건을 가치순으로 정렬
total_weight = 0
total_value = 0
stolen_items = []
for item in items:
if total_weight + item[1] <= hand_limit: # 아직 손에 들 수 있는 무게가 남아있는 경우
total_weight += item[1]
total_value += item[2]
stolen_items.append(item[0])
print("훔친 물건:", stolen_items)
print("총 훔친 물건의 가치:", total_value)
end_time = datetime.now()
elapsed = elapsed_time(start_time)
print("코드가 실행되는데 걸린 시간:", elapsed)출력결과
훔친 물건: ['아이폰', '아이패드에어', '컴퓨터 알고리즘 책', '애플워치']
총 훔친 물건의 가치: 3700
코드가 실행되는데 걸린 시간: 0:00:00.000035
DP 링크
from datetime import datetime
def elapsed_time(start_time):
end_time = datetime.now()
elapsed = end_time - start_time
return elapsed
def knapsack(items, hand_limit):
# 아이템의 개수와 손에 들 수 있는 최대 무게
n = len(items)
dp = [[0] * (hand_limit + 1) for _ in range(n + 1)]
# 다이나믹 프로그래밍을 통해 최적의 가치를 계산
for i in range(1, n + 1):
for w in range(1, hand_limit + 1):
weight, value = items[i - 1][1], items[i - 1][2]
if weight <= w:
dp[i][w] = max(dp[i - 1][w], dp[i - 1][w - weight] + value)
else:
dp[i][w] = dp[i - 1][w]
# 최적의 가치를 찾기 위해 역추적
total_value = dp[n][hand_limit]
total_weight = hand_limit
stolen_items = []
for i in range(n, 0, -1):
if dp[i][total_weight] != dp[i - 1][total_weight]:
item_name = items[i - 1][0]
stolen_items.append(item_name)
total_weight -= items[i - 1][1]
return stolen_items, total_value
start_time = datetime.now()
# 물건 종류, 무게, 가치
items = [
('아이폰', 2, 1100),
('컴퓨터 알고리즘 책', 1, 400),
('노트북', 10, 2000),
('아이패드프로', 5, 1800),
('아이패드에어', 3, 1500),
('애플워치', 2, 700)
]
# 손에 들 수 있는 무게
hand_limit = 10
stolen_items, total_value = knapsack(items, hand_limit)
print("훔친 물건:", stolen_items)
print("총 훔친 물건의 가치:", total_value)
end_time = datetime.now()
elapsed = elapsed_time(start_time)
print("코드가 실행되는데 걸린 시간:", elapsed)출력결과
훔친 물건: ['아이패드에어', '아이패드프로', '아이폰']
총 훔친 물건의 가치: 4400
코드가 실행되는데 걸린 시간: 0:00:00.000066
차이가 보임을 알 수 있습니다.
4. 코드모음
_링크_에 정리했습니다 참고 바랍니다:)
'3.4. 프로그래밍 개념 및 도구 > 알고리즘 이론' 카테고리의 다른 글
| [Algorithm] 다익스트라 알고리즘(Dijkstra Algorithm) (0) | 2024.04.08 |
|---|---|
| [Algorithm] 최소 신장 트리(MST), Kruskal & Prim algorithm (0) | 2024.04.07 |
| 3 다이나믹 프로그래밍(Dynamic Programming : DP/동적계획) (0) | 2024.04.07 |
| 2 정복분할(divide and conquer) (0) | 2024.03.30 |
| 1 Algorithm (0) | 2024.03.30 |


댓글